研究背景：

桩-土相互作用使得桩基础的地震响应非常复杂。由于桩基础的抗震性能直接决定了受支上部结构的安全性。因此，研究桩-土体系的地震响应是十分必要的。国内外的学者针对桩-土体系的解析方法进行了大量的研究（如，BDWF模型、改进Vlasov模型等）。改进Vlasov模型通过采用精确的桩土阻力，极大地改进了BDWF模型，但由于在求解过程中采用了迭代逼近，仍然不能提供严格的解析解。本研究的主要目的是推导端承桩竖向运动响应的严格解。与BDWF模型和改进Vlasov模型相比，本模型具有更简洁、明确的物理意义。并且在给出严格解的基础上，对桩土参数对桩土系统动力响应的影响进行了参数化研究。

研究方法及结果：

1.本文首先基于Vlasov法推导了一个新的桩-土动力阻抗模型。

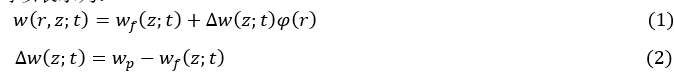
式中，W_f(z;t)是自由场位移，W_p(z;t)是桩位移，∆w(z;t)是桩和桩周土的相对位移，φ(*)是桩周散射场分布形状函数。

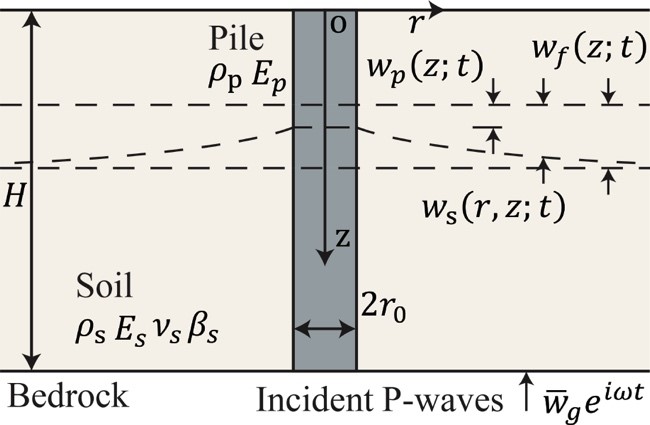
图1. P波入射桩-土体系模型

对某深度z 处dz厚的土层薄片进行能量分析，有：

由Hamilton原理，可以得到桩-土阻抗函数（模型）：

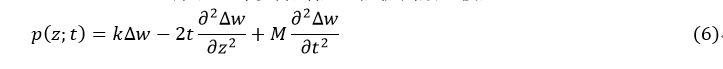
上述桩-土阻抗模型参考了Vlasov模型引进了能够简化连续介质基本方程的位移约束（桩-土散射场分布形状函数），基于连续介质方程推导而得。该桩-土阻抗模型是一种特殊的“双参数”模型，可以弥补以Winkler模型为代表的“单参数”模型无法描述土体连续性的固有缺陷；带入傅立叶级数展开的桩-土位移函数，即可得到简洁的桩-土弹簧模型；该模型仅包含两部分（Winkler弹簧和动力膜弹簧）（图2）。

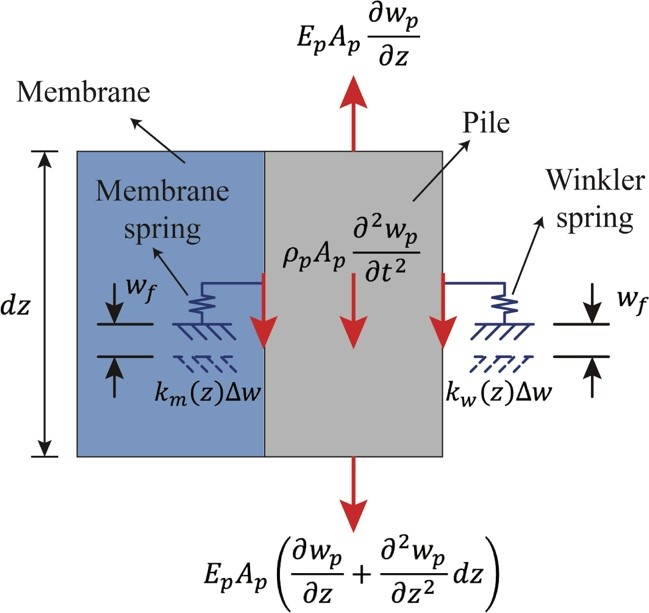
图2. 桩-土阻抗模型

2、本文研究了各参数对-桩弹簧系数、桩身动力响应的影响。

图3给出本文方法和其他方法（BDWF法，修正Vlasov模型）得到的运动学响应因子。本文方法被在数学上是严谨的，可用于验证其他方法的准确性。当桩-土刚度比较大(E_p/E_s=1000)时，本方法的预测结果与其他解吻合较好。而当桩-土刚度比较小(E_p/E_s=100) 时，桩周土对桩的约束较强。此时，桩土阻力对桩的地震反应有重要影响。BDWF和修正Vlasov模型的预测结果与本文方法有显著差异。

图4为不同特征刚度下桩体运动响应因子。桩的运动响应主要取决于桩的特征刚度，运动响应因子的变化趋势呈现出两种不同的形式:(a)当特征刚度较小（R≤2）时，运动响应系数随归一化频率的增加而周期性变化;(b)当特征刚度较大（R≥3）时，运动响应系数呈单调性减小。这说明刚性桩的响应对频率更为敏感。

图5为不同特征刚度下的桩动位移幅值。桩的变形主要取决于特征刚度：对于特征刚度较小的刚性桩，桩底相对位移较小；而随着特征刚度的增大，桩身位移增大，并趋于自由场。

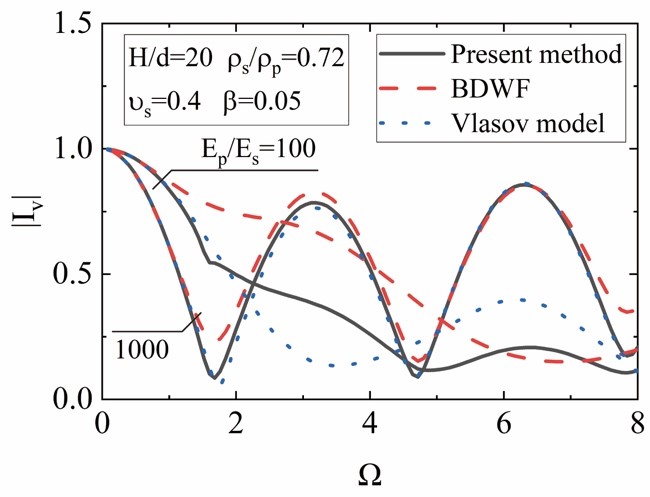
图3. 不同方法得到运动响应因子对比

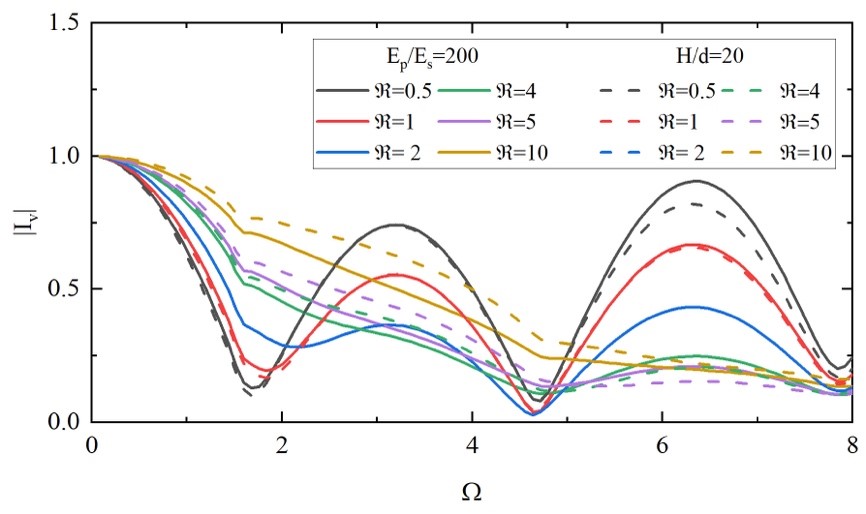
图4. 桩-土模量比和桩柔度系数对运动响应因子的影响

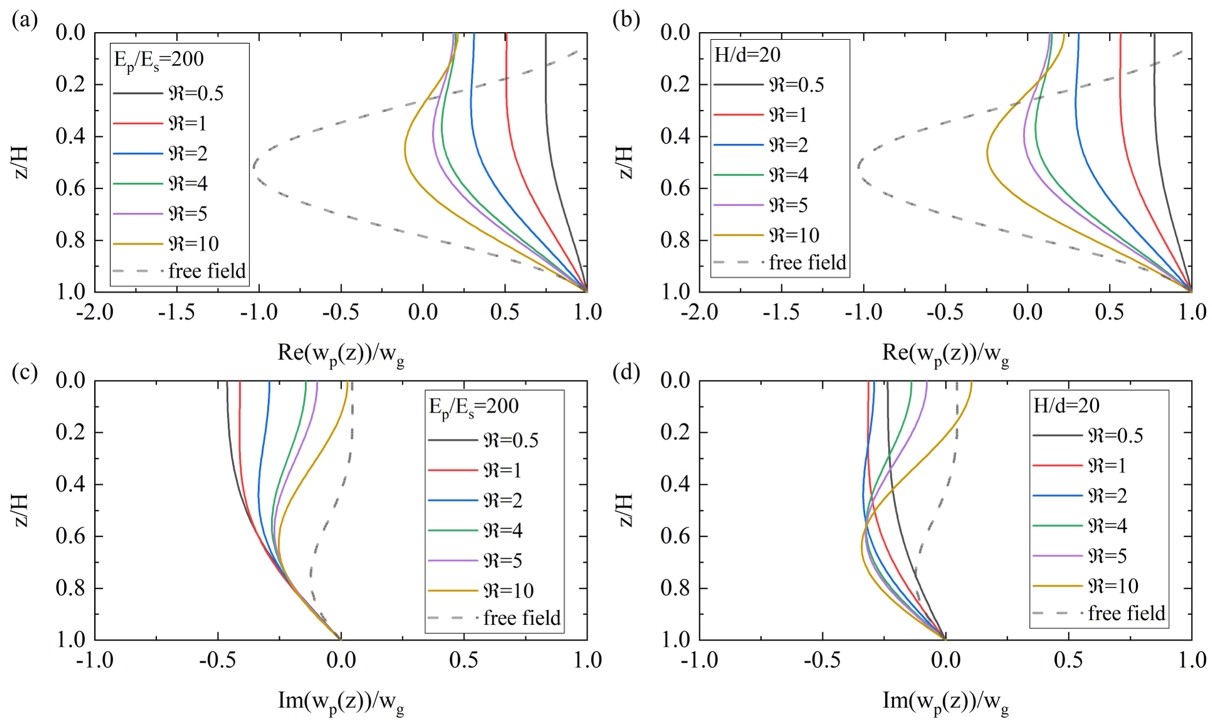
图5. 桩身位移响应

该成果发表在国际权威期刊《Computers and Geotechnics》（Dong Rui, Shan Zhendong^*, Jing Liping, Xie Zhinan, Zhiyong Yin, Zheng Tong. Rigorous solution for kinematic response of end-bearing pile under vertically incident P-waves, 2022, 150: 104896）（JCR影响因子：5.218 Q1，中科院分区表升级版1区Top期刊，*通讯作者）。